9022. Подсчитайте тройки

 

Заданы три массива a, b и c, каждый состоит из n целых чисел. Найдите количество троек (ai, bj, ck) таких что ai < bj < ck.

 

Вход. Первая строка содержит размеры массивов n. Вторая строка содержит элементы массива a. Следующая строка содержит элементы массива b. Последняя строка содержит элементы массива c.

 

Выход. Выведите количество троек (ai, bj, ck) таких что ai < bj < ck.

 

Пояснение. В первом тесте искомыми тройками будут (a1, b1, c1), (a1, b2, c1) и (a1, b2, c2).

 

Пример входа 1

Пример выхода 1

2

1 5

4 2

6 3

3

 

 

Пример входа 2

Пример выхода 2

3

1 1 1

2 2 2

3 3 3

27

 

 

РЕШЕНИЕ

бинарный поиск

 

Анализ алгоритма

Отсортируем массивы. Для каждого значения bj при помощи бинарного поиска находим количество чисел x из массива а, меньших bj, а также количество чисел y из массива c, больших bj. Тогда для фиксированного значения bj существует x * y искомых троек (ai, bj, ck).

 

Пример

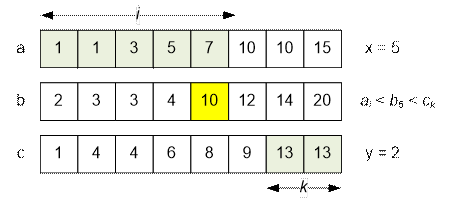
Рассмотрим следующие отсортированные массивы. Вычислим количество искомых троек, в которых b5 = 10. Имеем: ai < b5 при i ≤ 5, ck > b5 при k ≥ 7. То есть неравенство ai < b5 < ck имеет место для 1 ≤ i ≤ 5 и 7 ≤ k ≤ 8. Количество троек (ai, b5, ck) равно 5 * 2 = 10.

 

 

Реализация алгоритма

Объявим рабочие массивы.

 

#define MAX 100000

int a[MAX], b[MAX], c[MAX];

 

Читаем входные массивы.

 

scanf("%d", &n);

for (i = 0; i < n; i++) scanf("%d", &a[i]);

for (i = 0; i < n; i++) scanf("%d", &b[i]);

for (i = 0; i < n; i++) scanf("%d", &c[i]);

 

Сортируем массивы.

 

sort(a, a + n);

sort(b, b + n);

sort(c, c + n);

 

Количество искомых троек подсчитываем в переменной res. Перебираем значения bj.

 

res = 0;

for (j = 0; j < n; j++)

{

 

Количество чисел из массива a, меньших bj, равно x.

 

  x = lower_bound(a, a + n, b[j]) - a;

 

Количество чисел из массива c, больших bj, равно y.

 

  y = n - (upper_bound(c, c + n, b[j]) - c);

 

Для значения bj существует x * y искомых троек.

 

  res += x * y;

}

 

Выводим ответ.

 

printf("%lld\n", res);

 

Java реализация

 

import java.util.*;

 

public class Main

{

  static int lower_bound(int m[], int start, int end, int x)

  {

    while (start < end)

    {

      int mid = (start + end) / 2;

      if (x <= m[mid])

         end = mid;

      else

        start = mid + 1;

    }

    return start;

  }

 

  static int upper_bound(int m[], int start, int end, int x)

  {

    while (start < end)

    {

      int mid = (start + end) / 2;

      if (x >= m[mid])

        start = mid + 1;

      else

        end = mid;

    }

    return start;

  }

 

  public static void main(String[] args)

  {

    Scanner con = new Scanner(System.in);   

    int i, n = con.nextInt();

    int a[] = new int[n];

    for(i = 0; i < n; i++) a[i] = con.nextInt();

 

    int b[] = new int[n];

    for(i = 0; i < n; i++) b[i] = con.nextInt();

 

    int c[] = new int[n];

    for(i = 0; i < n; i++) c[i] = con.nextInt();

 

    Arrays.sort(a); Arrays.sort(b); Arrays.sort(c);

   

    long res = 0;

    for (i = 0; i < n; i++)

    {

      int x = lower_bound(a, 0, n, b[i]);

      int y = n - (upper_bound(c, 0, n, b[i]));

      res += 1L * x * y;

    }

   

    System.out.println(res);

    con.close();

  }

}